Support Vector Machines (SVM) are a potent type of supervised algorithm. These algorithms gained immense popularity in the 1990s and have since remained a top choice for high-performance machine learning models, requiring minimal tuning.
This post provides you with a proper understanding of Support Vector Machines, how they work, their types, and both the advantages and disadvantages of this essential machine learning tool.
Table of Contents
What Is A Support Vector Machine?
A Support Vector Machine (SVM) is a powerful machine learning algorithm that is especially effective in solving binary classification and regression problems, operating under the supervision of provided data.
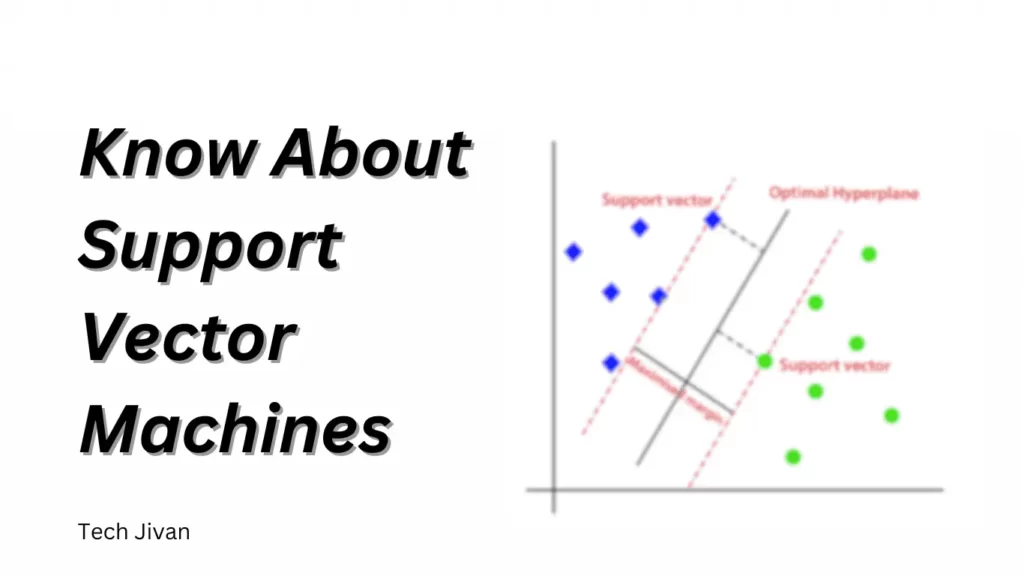
Its primary goal is to identify the optimal decision boundary, known as a hyperplane in high-dimensional spaces, to separate data points into different classes.
SVMs achieve this by maximizing the margin, which is the distance between the hyperplane and the nearest data points of each class, facilitating clear classification.
Support Vector Machines are particularly valuable when dealing with intricate data patterns that a simple straight line cannot separate.
In such cases, nonlinear SVMs employ a mathematical technique to transform the data into a higher-dimensional space, making it easier to find an effective boundary.
How Do Support Vector Machines Work?
Support Vector Machines (SVMs) operate by transforming input data into a higher-dimensional feature space, simplifying the task of finding a linear separation or better data classification.
This transformation is achieved using a kernel function, which calculates dot products between transformed feature vectors without explicitly determining the new coordinates, saving computational resources.
SVMs are versatile, handling both linear and non-linearly separable data through kernel functions like linear, polynomial, or radial basis function (RBF). These kernels empower SVMs to capture intricate data relationships effectively.
Support Vector Machines employs a mathematical approach to identify the optimal hyperplane in the higher-dimensional kernel space during training.
This hyperplane is pivotal because it maximizes the margin between different class data points while minimizing classification errors.
The choice of kernel function profoundly impacts SVM performance, requiring careful selection based on the specific data characteristics.
What Are The Kernel Functions For Support Vector Machines
Support Vector Machines (SVMs) employ various kernel functions to handle different types of data:
1. Linear Kernel: The simplest of all, this function transforms data into a higher-dimensional space to make it linearly separable.
2. Polynomial Kernel: More versatile than the linear kernel, it can handle non-linearly separable data by mapping it to a higher-dimensional space.
3. RBF Kernel: Among the most popular, this kernel is effective for a wide range of classification problems due to its flexibility.
4. Sigmoid Kernel: Similar to the RBF kernel, it has a distinct shape that can be advantageous for certain classification challenges.
The choice of kernel depends on the balance between accuracy and complexity. More powerful kernels like RBF can provide better accuracy but may require more data and computation during SVM training.
However, technological advancements have mitigated this concern. After training, SVMs classify new data points by determining which side of the decision boundary they belong to, and the output is the associated class label.
Read Also: The 7 Best AI Code Generator Tools For Programmers
What Are The Types Of Support Vector Machines
Support Vector Machines encompass various types tailored to specific needs. Let’s explore two prominent types and their respective purposes:
1. Linear Support Vector Machines:
Linear SVMs employ a linear kernel to establish a straight-line decision boundary, segregating different classes. They shine when dealing with linearly separable data or when a simple approximation suffices.
Linear SVMs are known for their computational efficiency and straightforward interpretability, as they delineate the decision boundary as a hyperplane within the input feature space.
2. Nonlinear Support Vector Machines:
Nonlinear SVMs come into play when data cannot be neatly separated by a straight line in the feature space.
These SVMs tackle this by employing kernel functions, which implicitly map the data into a higher-dimensional feature space.
A linear decision boundary can be located in this higher-dimensional space, even for intricate data distributions. Commonly used kernels include the polynomial, Gaussian (RBF), and sigmoid kernels.
Nonlinear SVMs excel at capturing intricate patterns and typically yield higher classification accuracy compared to their linear counterparts.
Advantages And Disadvantages Of Support Vector Machines
The Advantages Of Support Vector Machines
Support Vector Machines (SVMs) offer several main advantages:
- SVMs excel in scenarios where you have more features than data points, making them suitable for high-dimensional datasets.
- SVMs are less susceptible to this issue than some algorithms prone to overfitting. They prioritize generalization, ensuring robust performance on new data.
- Support Vector Machines are versatile and applicable to both classification and regression problems.
- They accommodate various kernel functions, allowing for capturing intricate data relationships.
- Support Vector Machines have the ability to handle non-linearly separable data by utilizing kernel functions.
- SVMs perform well with small training datasets. By focusing on support vectors, they leverage a subset of data points to determine the decision boundary, which is beneficial when data is scarce.
Read Also: How Long Can We Screen Record on iPhone
The Disadvantages Of Support Vector Machines
Support Vector Machines (SVMs) are favored for their strengths, but it’s important to acknowledge their disadvantages:
- Demand substantial computational resources, especially with sizable datasets. Training time and memory requirements rise significantly as the dataset grows.
- Support Vector Machines involve parameter tuning, including the regularization parameter and kernel function choice.
- The model’s performance hinges on these settings, making improper tuning result in suboptimal outcomes or extended training times.
- Yield binary classification outputs, lacking direct class probability estimation. Additional techniques, like Platt scaling or cross-validation, are necessary to derive probability estimates.
- SVMs can establish intricate decision boundaries, notably with nonlinear kernels. This complexity can impede model interpretation, making it challenging to grasp underlying data patterns.
- Encounter scalability issues when handling exceptionally large datasets. Training an SVM on millions of samples becomes impractical due to memory and computational limitations.
Conclusion
Through this article, we tried to guide you on all the important points related to Support Vector Machines (SVMs). We have mentioned types, advantages, and disadvantages of Support Vector Machines (SVMs). We hope you liked this article; share it with your friends also.
Frequently Asked Questions
Q. What are the key steps in Support Vector Machines?
Ans: The Support Vector Machines process includes:
- Choosing the right kernel function.
- Defining parameters and constraints.
- Solving an optimization problem to find the optimal hyperplane.
- Making predictions based on the model.
Q. What does the SVM algorithm do?
Ans: SVM is an algorithm used for both classification and regression. It identifies the best hyperplane to separate data points of different classes in high-dimensional space.
Q. What’s the role of SVM in machine learning?
Ans: SVM is used in machine learning to classify data by finding the ideal decision boundary that maximizes the separation between different classes. It’s effective even in complex, nonlinear scenarios by maximizing the margin between support vectors.
Q. Why are support vector machines considered a top algorithm?
Ans: Support vector machines stand out because they can handle high-dimensional data, excel with limited training samples, and perform nonlinear classification through kernel functions.






